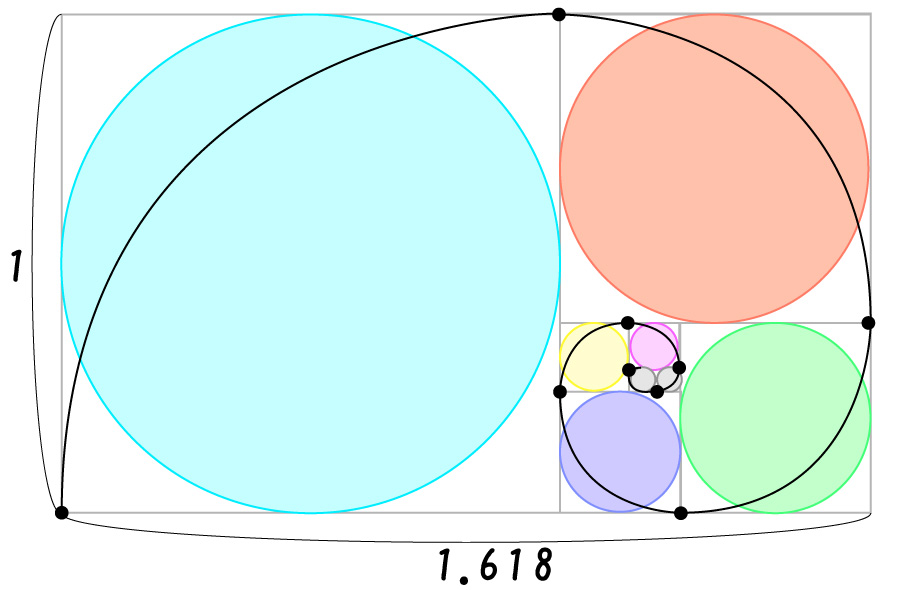
皆さんは黄金比を知っていますか？
デザイナーさんは知っている方も多いと思います。

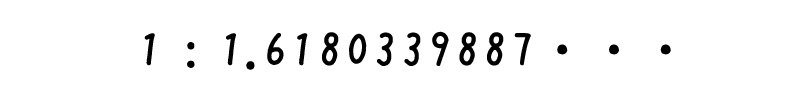
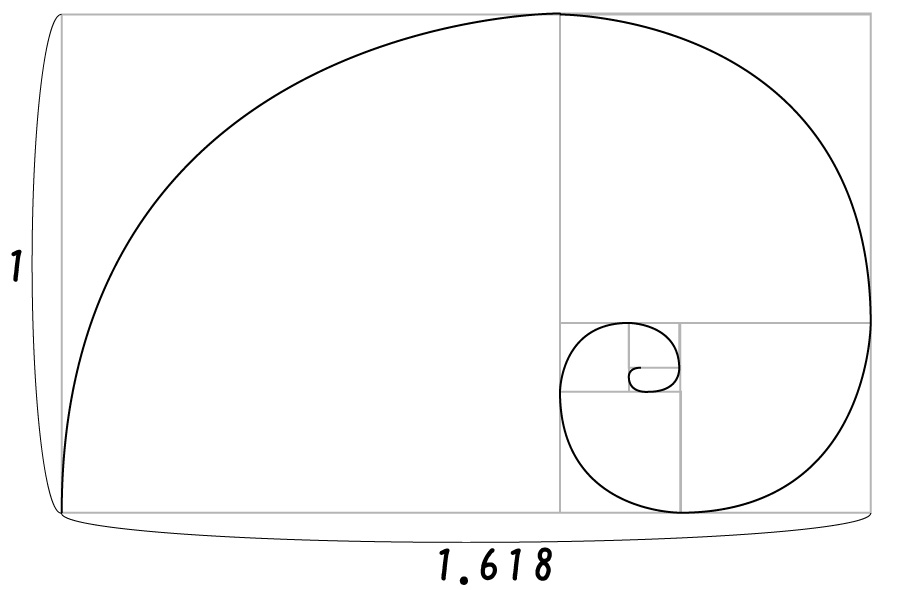
この図形の方が知っている人は多いですかね？
黄金比によってできる「黄金長方形」「黄金螺旋」です。

デザインの世界では黄金比は、最も美しく感じられる比率とされているそうです。

黄金比がどのようにデザイン的に美しいのか、どんな場面で黄金比が使われたり、
「実はこれも黄金比だった」というような事例についてはここでは割愛させていただいて。

この記事では、「黄金比をフィボナッチ数列から求める」にフォーカスを当てようと思います！

内容としては、「数学」や「幾何学」という（難しそうな）学問ではなく、小学校で勉強する「算数」です！

• 1.フィボナッチ数列って？
• 2.フィボナッチ数列が黄金比に近づいていく
• 3.フィボナッチ数列が黄金曲線に近づいていく
• 4.おまけの数学的な楽しみ方
• まとめ

この黄金比に出てくる「1.6181…」と言う数は、フィボナッチ数列というものから導くことができるそうです。

（ここで、「できるそうです」と書いたのは、私は数学のプロでも幾何学のプロでもないので、ここに書く内容は言い回しや表現が曖昧で、証明しているわけでも断言しているわけでもないからです！あくまでも、フワっとした考察をしているだけですのでご了承ください！）

1. フィボナッチ数列って？

さて、フィボナッチ数列とは、

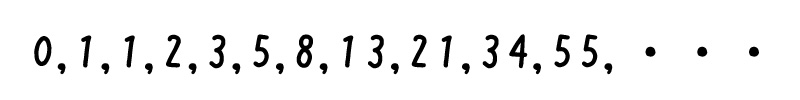
次の項（数字）は、前の2項の和で求められる、そんな数の列です。

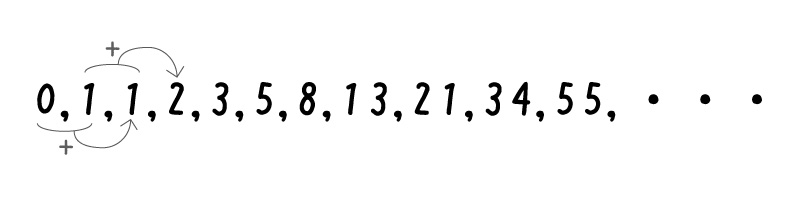
前の2項を足すと次の項が出てくるので、終わりがありません。

莫大な桁数の数と莫大な桁数の数であっても、それは足し算可能なので、次の数も莫大な桁数ですが、求められます。

と、そんな無限に続くフィボナッチ数列ですが、どこが黄金比と結びつくのでしょう？

2. フィボナッチ数列が黄金比に近づいていく

この数列の中の数を使って計算遊びをしてみましょう！（電卓があると良いヨ）

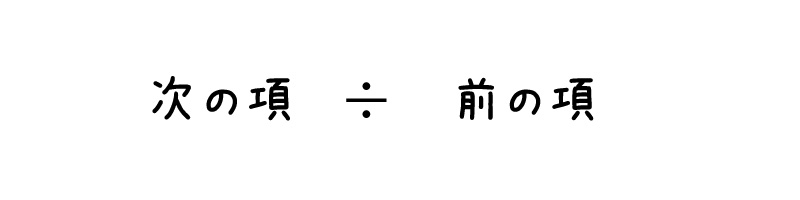
「次の項÷前の項」を順々に繰り返して、また新しい数列を作ってみます。

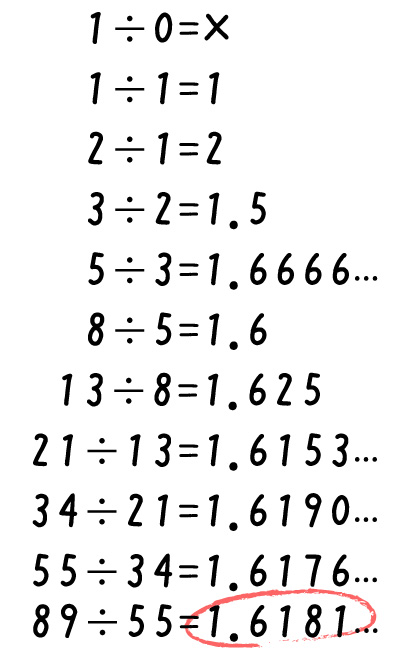
するとだんだん、黄金比の「1:1.618…」に近い数字が出てくるのです！
※「1÷0=×」なのは何故か、については、話が脱線してしまうため割愛します。。

この先どんどん割り算を進めると、もっともっと近づきます。
（例えば下記は、第39項と第40項の割り算です。ほとんど黄金比の数ですね）

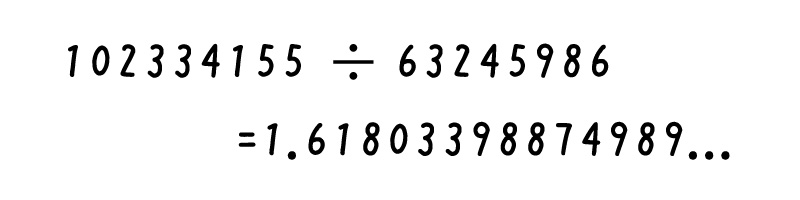
このように、フィボナッチ数列と黄金比は、関係が深いようです…！

3. フィボナッチ数列が黄金曲線に近づいていく

では次に、黄金曲線が描かれている下記の図形について考えていきましょう。
今度は数列から、幾何学で遊んでみます！

まずは、フィボナッチ数列をもう一度見てみます。

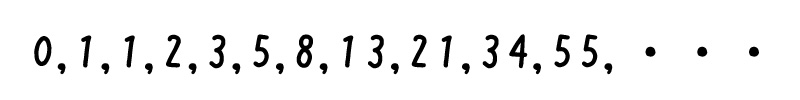
この数字と同じ直径を持つ円を、下記のように並べてみます。

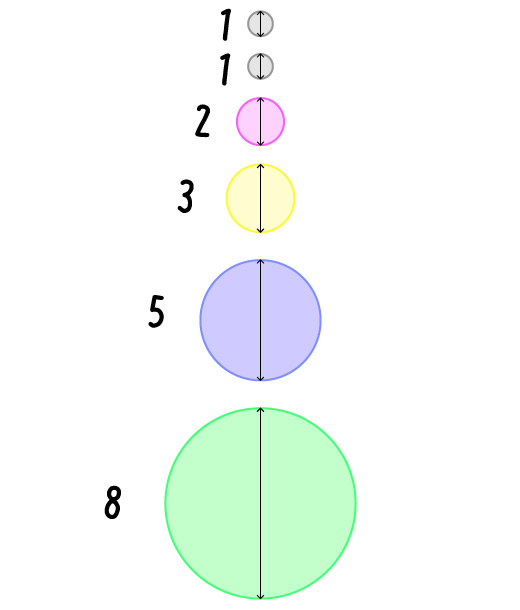
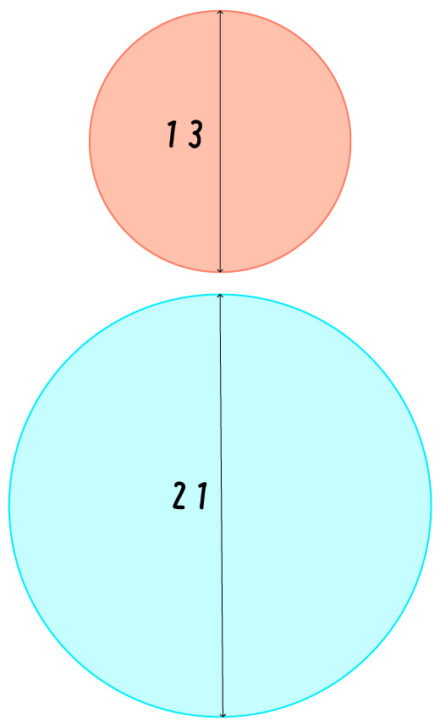
さて、この並んだ円を敷き詰めるように並べてみると…

そして、この円を囲うように正方形で囲みます。

そうすると、この長方形の縦と横の比率は「1.1618」になります。

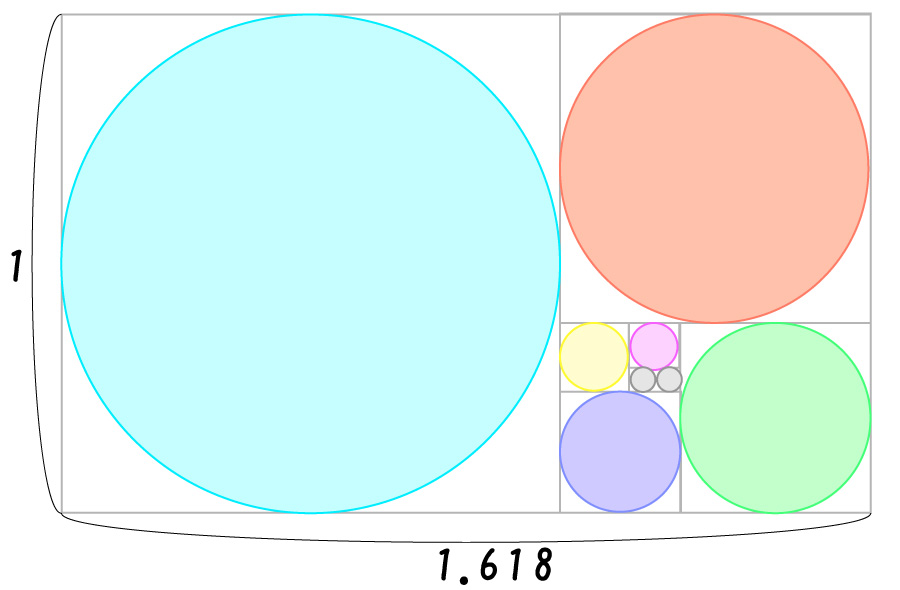
左端から、正方形の逆端に点を付けます。

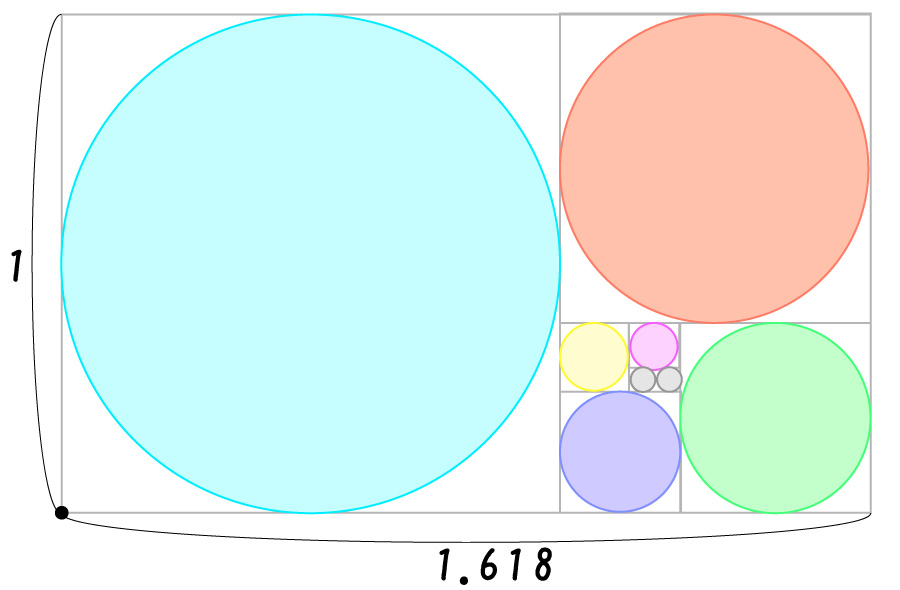
逆端だった点から、また次の正方形の逆端に点をつけます。

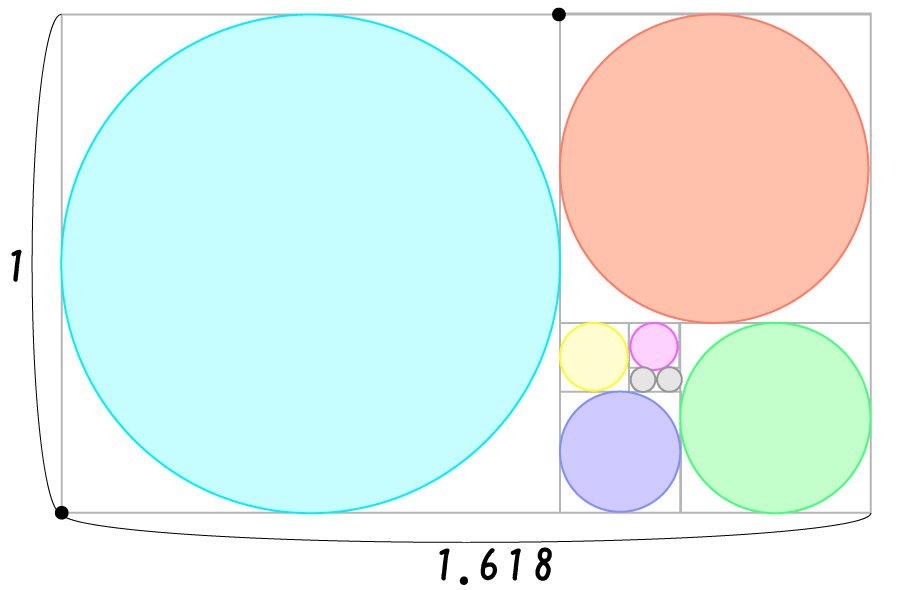
こんな感じで、次の正方形の逆端に、次の正方形の逆端に…と、どんどん点をつけます。

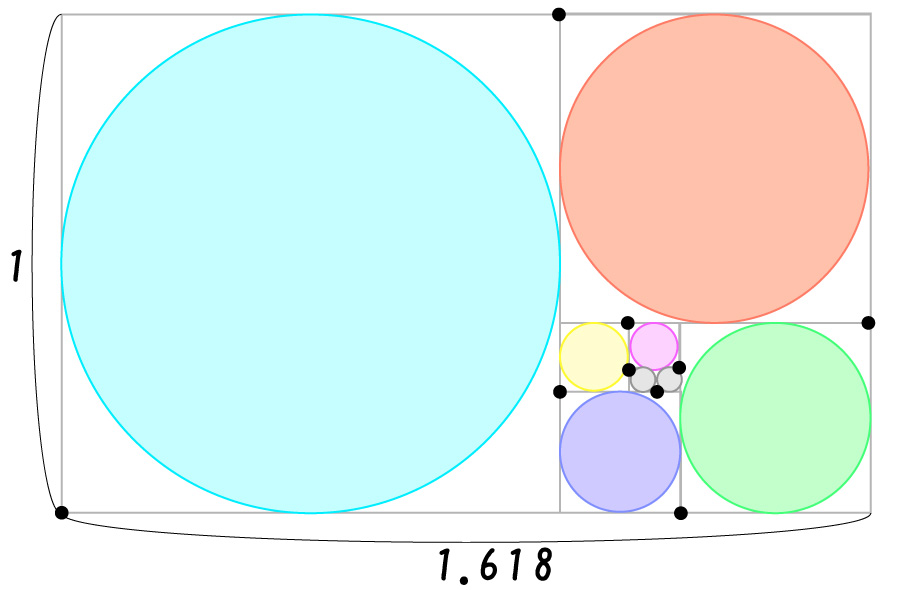
最後にこの点を通るように、滑らかな線で繋げると

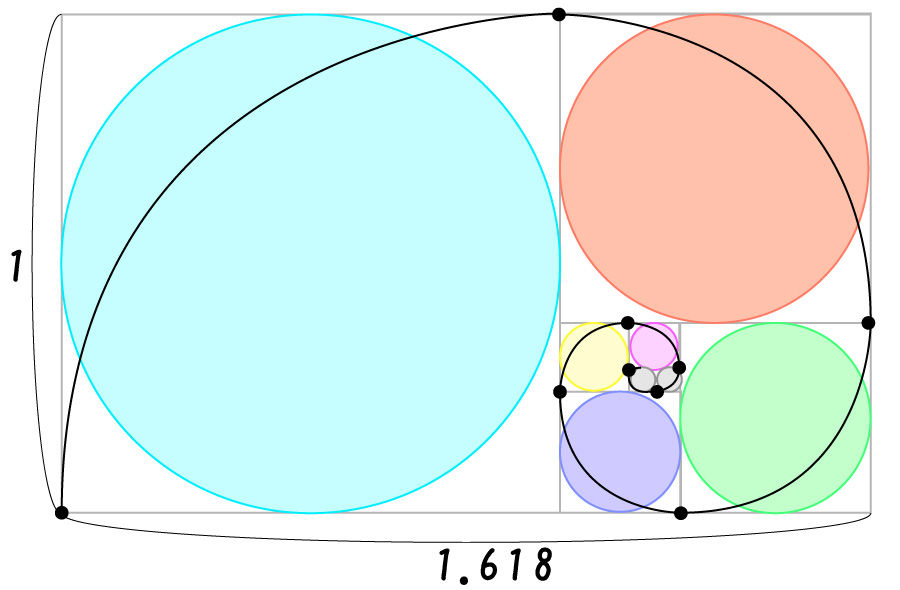
黄金螺旋の出来上がり！！

こんな感じで、フィボナッチ数列と黄金比＆黄金螺旋は、とっても仲良しなんですね！

4. おまけの数学的な楽しみ方

さて、ここからはおまけの楽しみ方です。

フィボナッチ数列を「次の項÷前の項」して行った時のこの答えたちをグラフにしてみました。すると…

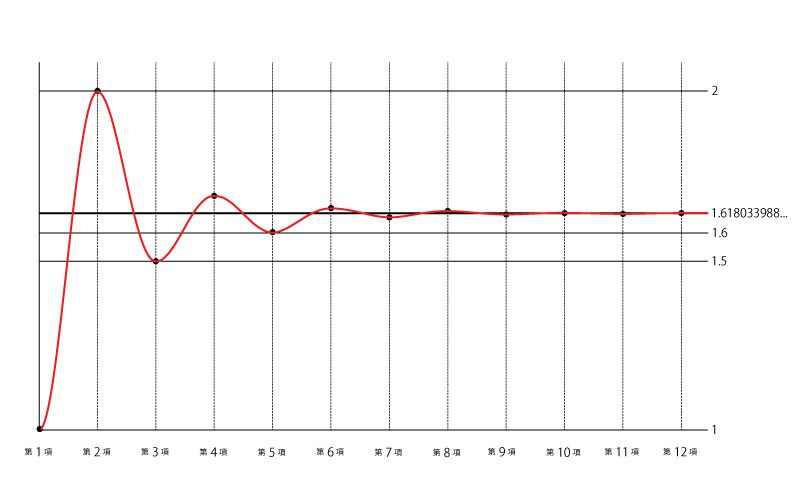
そうすると、1.618……という黄金比にだんだん近づくときに、
このグラフのように、上下にふらふら（振動）しながら近づいていくんです！

「黄金比にだんだん近づく」と一言で言っても

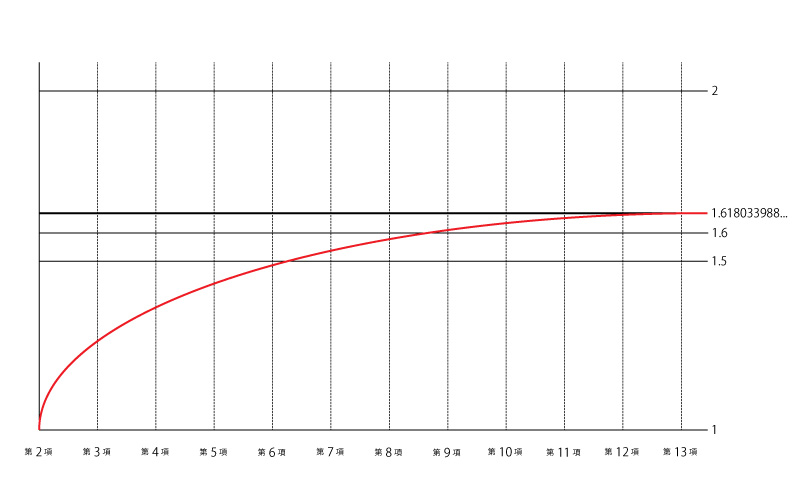
こんなふうでもなく

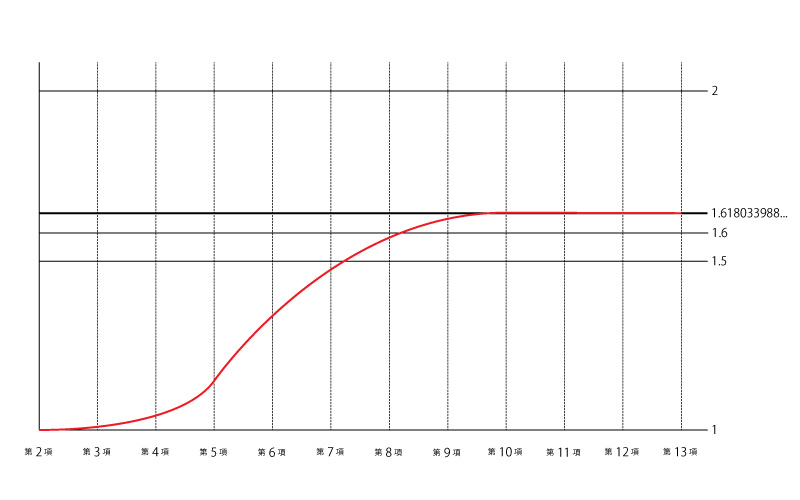
こんなんでもない、

こんなふうに振動しながら近づくんですね！

電卓で手作業で計算すると、こんなことがよくわかります！楽しい♪

まとめ

いかがだったでしょうか？

実はこのサイト「BOTAO」のロゴも、黄金比だったりします。

今回私は「黄金比」と「フィボナッチ数列」が関係していることは、既に「黄金比」について調べた時に書いてあった情報で知っていたのですが、

「なぜ関係しているのか？」は、他の方が書いた記事などをさらっと読んだだけでしたので、うっすらしか理解していませんでした。

「うっすら知った情報」は、瞬く間に記憶から削除され（笑）ていましたが、
今回自分で探ってみて、自分で黄金比曲線を描いてみることで、
前とは随分違う根深いところまで、記憶に染み渡った感覚があります。

そして何より、自分の手（電卓）を使って探ることによって、
（たとえそれが、多くの人が既に知っている情報だったとしても）
「わ〜、楽しいなー！！」と思えました。

「自分でやってみる」ことへの大きな意味があったと言えますね！